主成分分析（PCA）是一种对数据进行降维，并尽可能保留更多信息的方法。在PCA中，衡量信息的多少的指标是变量的 “分散” 程度。例如，考虑以下数据：

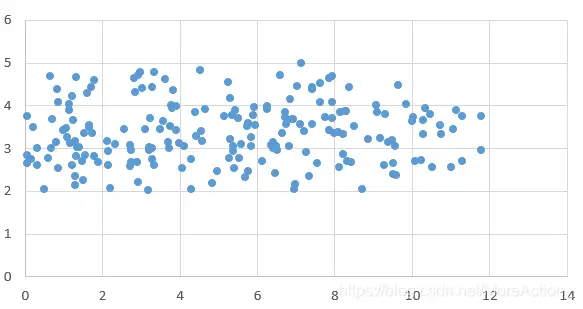
X轴上的分散程度远远大于Y轴上的，因此我们认为X轴上蕴含的信息比Y轴上要多。而为了衡量数据在某个轴上的分散程度，一个自然的想法是求出数据在该轴上的方差。而PCA的思想，就是建立一个新的 $m$ 维坐标系，使得在新坐标系各坐标轴上数据的方差尽量大。

数学推导

设有一列数据 $\{X_n\}$ ，那么问题转化为，求出一个单位向量 $w$，使得这些数据在这个向量方向上的投影长度的方差最大。由于 $w$ 是单位向量，$X_i$ 在 $w$ 方向上投影的长度就是 $w^T{X}_i$ 。 因此可以列式如下：

$$D(X)=\frac{1}{n}\sum _{i=1}^n(w^T{X}_i-w^T\bar{X}{)}^2$$

其中涉及到 $\bar{X}$ ，为了计算方便，不妨对 $X$ 进行去中心化：$X_i^{\prime }=X_i-\bar{X}$ 。则式子变成下面的形式：

$$\begin{array}{rl}D(X)& =\frac{1}{n}\sum _{i=1}^n(w^T{X}_i^{\prime }{)}^2\\ & =\frac{1}{n}\sum _{i=1}^n(w^T{X}_i^{\prime })(w^T{X}_i^{\prime }{)}^T\\ & =\frac{1}{n}\sum _{i=1}^n{w}^T{X}_i^{\prime }{X}_i^{\prime T}w\\ & =\frac{1}{n}{w}^T(\sum _{i=1}^n{X}_i^{\prime }{X}_i^{\prime T})w\end{array}$$

其中，$\sum _{i=1}^n{X}_i^{\prime }{X}_i^{\prime T}=\sum _{i=1}^n(X_i-\bar{X})(X_i-\bar{X}{)}^T$ 是 $X$ 的协方差矩阵，不妨记作 $C$ ,则问题转化为在 $w^{T}w=1$ 的条件下，求 $w^{T}Cw$ 的最大值。因此使用拉格朗日乘子法，列出拉格朗日方程如下：

$$\mathcal{L}(w,\lambda )=w^{T}Cw-\lambda (1-w^{T}w)$$

求出偏导数并使其为 $0$ :

$$\{\begin{array}{l}\frac{\partial \mathcal{L}}{\partial w}=2Cw-2\lambda w=0\\ \frac{\partial \mathcal{L}}{\partial \lambda }=-(1-w^{T}w)=0\end{array}$$

因此：

$$\{\begin{array}{l}Cw=\lambda w\\ w^{T}w=1\end{array}$$

不难发现， $w$ 就是 $C$ 的特征向量，而 $\lambda$ 就是对应的特征值。带回到方差算式中：$D(X)=\frac{1}{n}{w}^{T}Cw=\frac{1}{n}{w}^T\lambda w=\frac{\lambda }{n}$ ，因此对 $C$ 作特征值分解后，取前 $m$ 大的特征值对应的特征向量，由于 $C$ 是对称的矩阵，因此特征向量间相互正交，那么将数据投影到这些向量的方向上就完成了PCA的过程。

numpy实现

import numpy as np

def PCA(data):
	data = data - data.mean(axis = 1, keepdims = True)
	C = np.dot(data,data.T)
	
	u,v,d = np.linalg.svd(C)
	
	return np.dot(u[:,:k].T, data)