Transformer

序列处理

我们时常期望能够基于已有的向量序列对接下来的向量进行预测、从序列中提取信息或从头生成一个新的序列。例如，我们可能期望预测一段文本接下来可能出现的字符，或是将一种语言翻译为另外一种。我们形式化一个序列如下：

$$
X:X_i \in R^d,i \in N^+
$$

其中 $d$ 是每个向量的维度。
因此可以将输入视为一个矩阵:

$$
X_{input} \in R^{n*d}
$$

其中 $n$ 是输入向量的数量。

自回归模型与隐变量自回归模型

根据直觉，我们很容易设计出一个基于全连结层的模型：

$$
X_{i+1} = f(X_i,X_{i-1},...,X_{i-r})
$$

即利用序列的前几项来预测序列的下一项。但实际上，由于预测误差的存在，$X_{i+1}$ 的真实表达式如下：

$$
X_{i+1} = f(X_i,X_{i-1},...,X_{i-r}) + \epsilon
$$

其中的 $\epsilon$ 是预测值相当于真实值的误差。当我们用带有误差的项预测接下来的项时，误差就会随预测的项数累积，这导致预测值很快会偏离真实值很多。

实际上，简单的自回归模型只能使用有限的几项来预测下一项，这导致在前面的项的信息完全被忽略了。基于此，人们引入了隐变量的概念。

隐变量可以视作对前面序列的总结，我们从前往后读取每一项后，都会用一个全连结层来更新隐变量，最后用隐变量来预测序列的下一项：

$$
h_i = \phi(h_{i-1},x_i)
$$
$$
Out = g(h_n)
$$

循环神经网络

循环神经网络(RNN)基于隐变量自回归模型，在普通的全连接层的基础上加入了隐变量，实现了对整个输入序列信息的利用。

设输入 $X_i \in R^{n*d}$ ，RNN使用 $H_i \in R^{n*h}$ 来描述隐变量，其中 $h$ 为隐藏层维度。在从前往后处理序列中每一个输入时，RNN先用前一步的隐变量和输入更新隐变量，然后用隐变量来得到输出。即：

$$
H_i = \phi(X_iW_{xh}+H_{i-1}W_{hh}+b_{hh})
$$
$$
O_i = H_iW_{hq} + b_q
$$

截断

由于RNN的每一次输出都依赖前一步的隐变量，而每次隐变量更新都会用到$W_{hh}$的值，这导致计算梯度时会用到 $W_{hh}$的潜在的高次幂，因此根据其特征值是否大于 $1$ 会发生梯度爆炸或梯度消失，并且计算代价也变得高昂，因此我们选择在这个链式计算中截断出后面几项进行近似计算。

截断可分为两种策略：随机截断和定长截断。定长截断即在向后传播指定步数后即结束，而随机截断则根据特定算法在一个随机的步数后结束。通常，我们使用定长截断来进行反向传播。

token,vocabulary与tokenize

对于一个文本序列，通常我们需要先确定我们在什么层面上进行处理，例如在语音识别中我们可能需要在字符层面上处理，而在翻译任务中则可能在词语层面上处理。

区分不同层面的是该层面中字符串的最小单元，称之为 Token。我们为每个 Token 分配一个编号，并建立一张 Token 到原始最小单元的表，称为 Vocabulary ，记作 $V$ ，而将原始字符串转化为 Token 编号的过程即为 Tokenization.

独热编码和嵌入层

如果直接将token视为神经网络的输入和输出，那么很小的扰动都可能使得输出的token的编号发生改变，并且神经网络处理的应该是数值变量而非分类变量，因此我们需要将token转化为一个向量。

独热编码是一个实现这一目的的简单方法，它将 token 映射为一个维度为词表大小 $|V|$ 的向量，具体来说，有：

$$
\begin{equation} X_i = \left\{
\begin{aligned}
0,token \neq i\\
1,token=i
\end{aligned} \right.
\end{equation}
$$

即一个只有第 $token$ 项为 $1$ ，其余为 $0$ 的向量。

独热编码只区分了不同的token，而嵌入层 (Embedding) 则更进一步根据语义调整了向量间的距离。嵌入层使用token经独热编码后的向量与一个矩阵相乘，得到不同token语义化的向量:

$$
X'_i = W_{embedding}X_i
$$

在输出时，可将输出向量应用softmax层视为各个token的概率。

门，LSTM与GRU

朴素的 RNN 的隐变量使我们可以保存序列前端的信息，但受限于隐变量的大小，保存的信息量是有限的。然而，可能并非序列中所有的信息都对未来同等重要，例如对于一个删去冠词的英文语句我们通常也能正确理解。同时，基于此，人们发明了可以选择性记忆的长短期储存器(LSTM)，并改进成为门控循环单元(GRU)。

LSTM和GRU都基于 "门" 的概念。具体来说，门可以表示为 $G \in [0,1]^{m*n}$，通过控制其中元素在 $[0,1]$ 间取值并与另一个矩阵（通常是隐变量）取阿达玛积可以控制该矩阵那哪元素可以“通过”从而参与接下来的运算。

LSTM由三种门控制：遗忘门，输入门和输出门。此外，相比于RNN，LSTM额外引入了隐变量 $C$ 来保存记忆。对于每一个输入 $X_t$，LSTM先使用遗忘门筛选出有用的记忆，然后使用输入门来获取新的记忆并更新 $C$，最后用输出门决定哪些记忆参与到输出中:

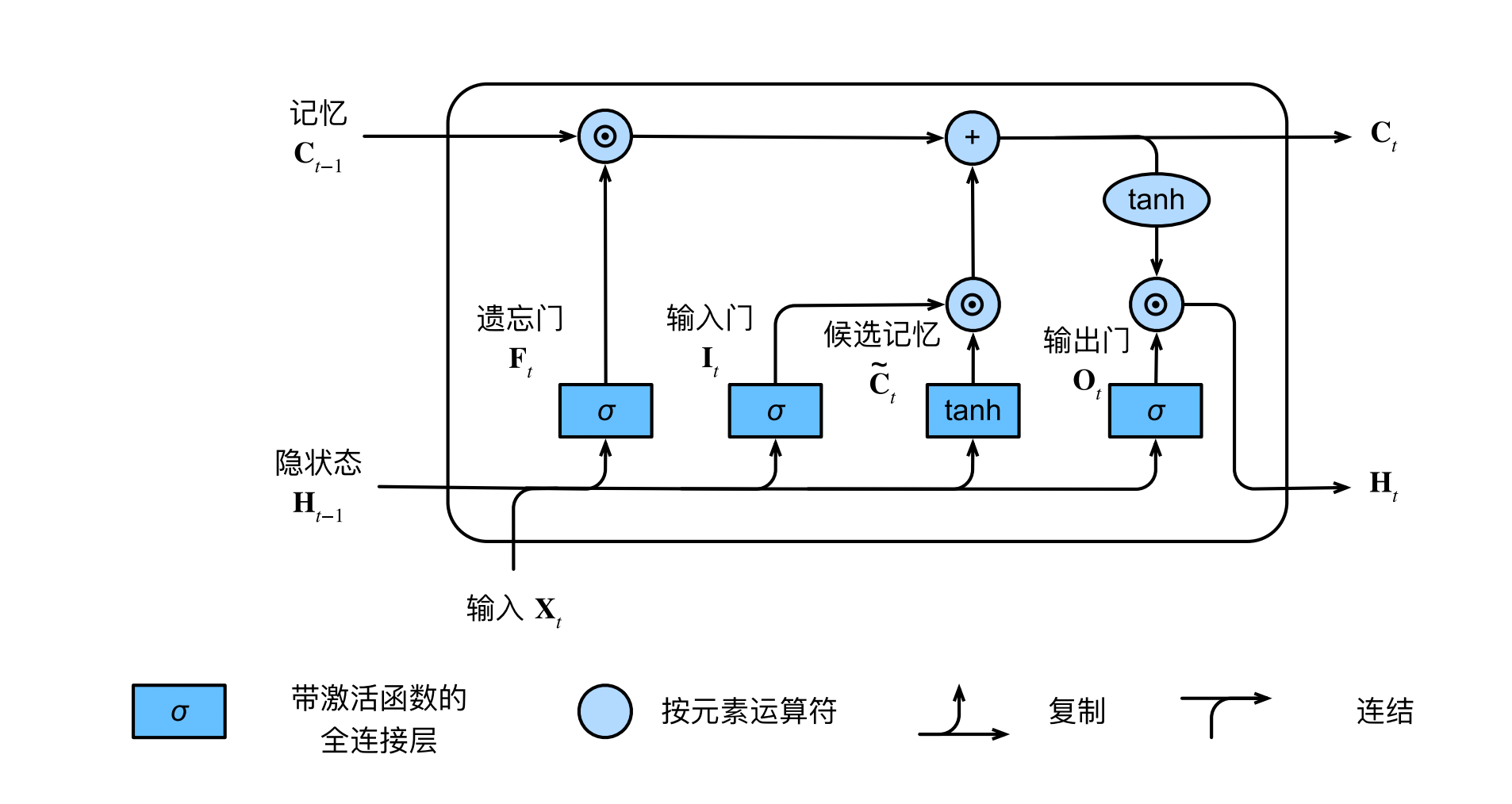
具体来说，LSTM在接受每个输入时，首先会更新各个门的隐变量值：

$$
\begin{align}
F_t &= \sigma(X_tW_{xf} +H_{t-1}W_{hf} +b_f)\\
I_t &= \sigma(X_tW_{xi} +H_{t-1}W_{hi} +b_i)\\
O_t &= \sigma(X_tW_{xo} +H_{t-1}W_{ho} +b_o)
\end{align}
$$

其中 $F$，$I$，$O$ 分别代表遗忘门、输入门和输出门。

然后，LSTM使用上一个隐状态和输入产生候选记忆，并使用输入门和遗忘门来更新记忆：

$$
\begin{align}
C_t' &= \tanh(X_tW_{xc}+H_{t-1}W_{hc}+b_c)\\
C_t &= F_t \odot C_{t-1} + I_t \odot C'_t
\end{align}
$$

其中$C'_t$ 是候选记忆。

最后，使用输出门决定使用哪些记忆参与输出：

$$
H_t = O_t \odot \tanh C_t
$$

而GRU将LSTM中的遗忘门和输出门整合为更新门，控制哪些记忆应该被更新，并取消了记忆隐变量 $C_t$。对于每个输入，GRU使用重置门来获得候选隐状态 $\overline H_t$，并用更新门来获得新的隐状态：

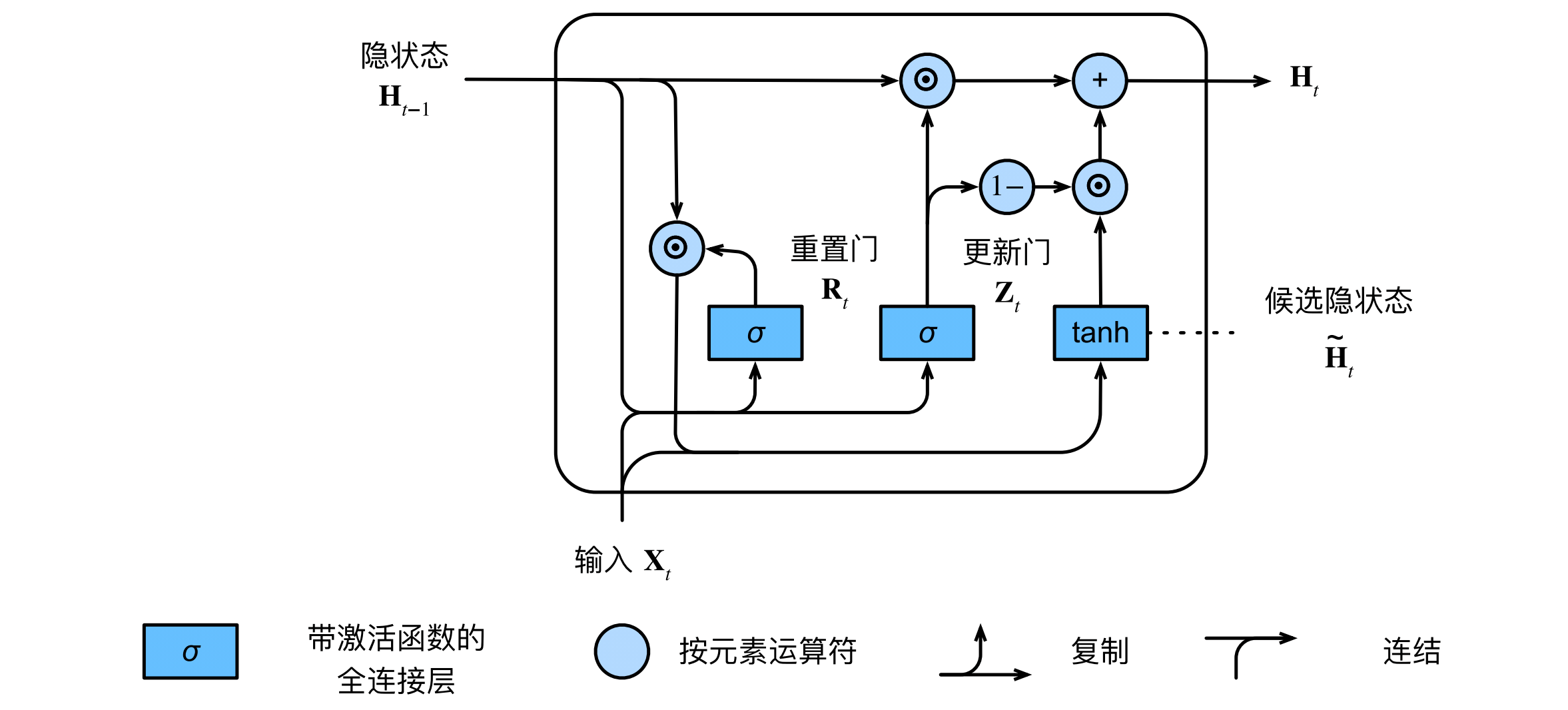
更新门和重置门的计算与LSTM类似：

$$
\begin{align}
R_t = \sigma(X_tW_{xr} + H_{t-1}W_{hr} + b_r)\\
Z_t = \sigma(X_tW_{xz} + H_{t-1}W_{hz} + b_z)
\end{align}
$$

其中 $R_t$ 代表重置门，$Z_t$ 代表更新门。
然后计算候选隐状态：

$$
\overline H_t = \tanh(X_tW_{xh} + (R_t \odot H_{t-1})W_{hh} + b_{hh})
$$

最后使用更新门更新隐状态：

$$
H_t = Z_t \odot H_{t-1} + (1-Z_t) \odot \overline H_t
$$

深度循环神经网络

将隐状态作为输入，并输入到另一个RNN中，称为深度循环神经网络。显然，相比于单层RNN，深度循环神经网络可以保存更多信息，并具有更高的灵活性：

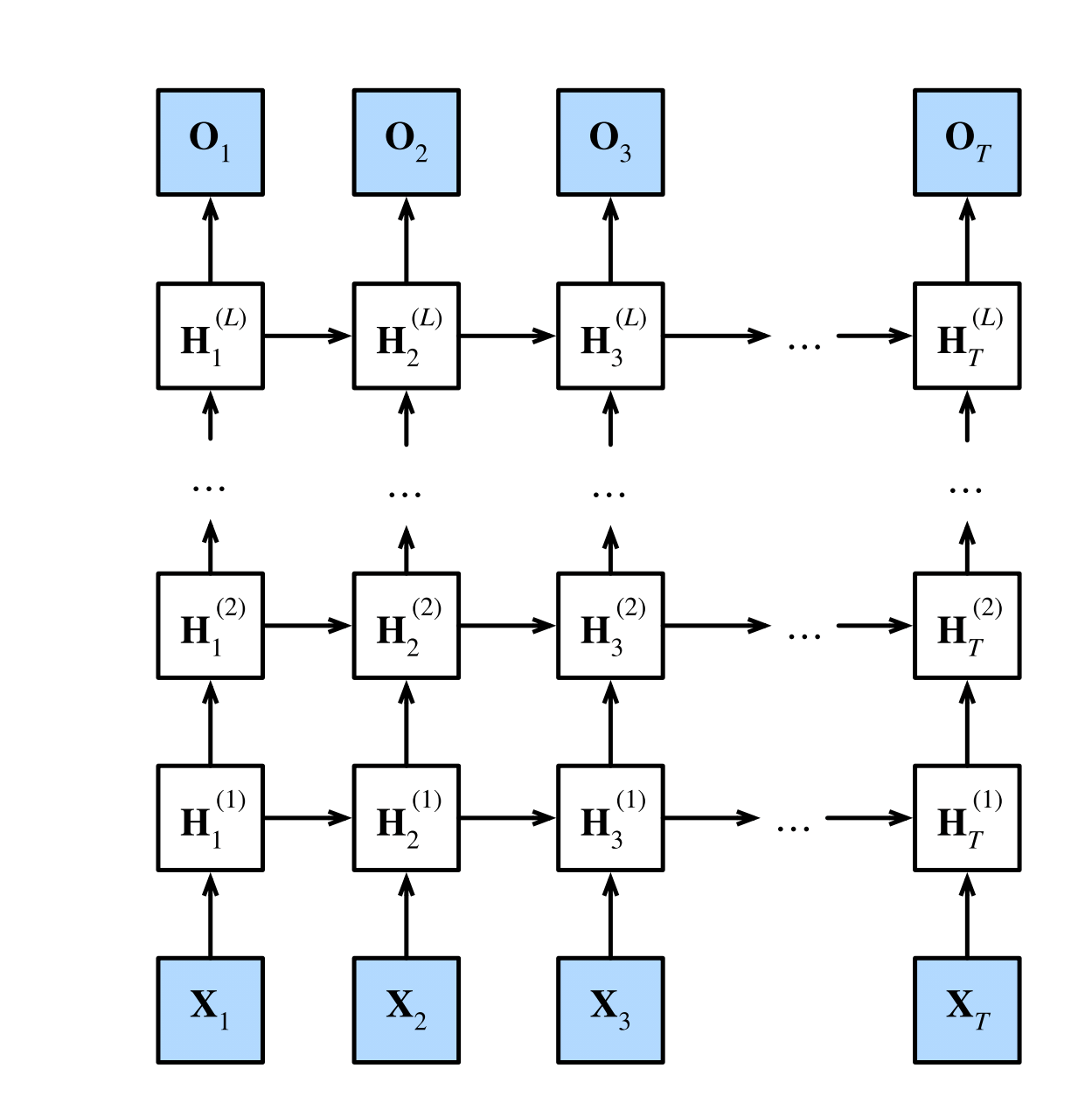
seq2seq任务、Encoder-Decoder架构

有时我们不希望预测序列的下一项，而希望根据已有序列生成一个新的序列。例如，我们可能希望将文字从一种语言翻译到另外一种。这种从序列生成新序列的任务称为seq2seq

通常，生成新序列时需要源序列的全部信息，因此人们提出了编解码器架构：

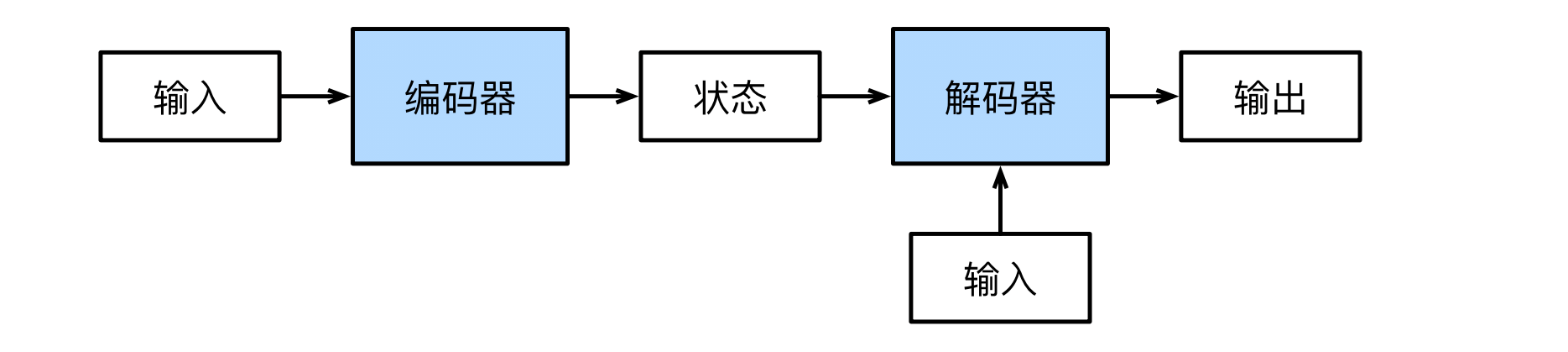
编码器将输入序列整合为一个状态，然后解码器从一个起始token开始，将输出再输入到自身，解码出整个序列。一般情况下，我们需要一些特殊的token来标识序列的开始和结束。

注意力机制

目前为止我们的RNN都是在被动的选择记忆进行输出，但在特定的上下文中，某些记忆可能对输出对其他记忆更重要，这提示我们根据上下文"查询"过去的记忆。因此，人们提出了注意力机制。

注意力机制可以看作一个字典，其中有若干键值对，记作$(K,V)$，通过注意力评分函数，对查询$Q$和记忆中每个键的匹配程度进行打分，并通过softmax得到每个值的权重，最后进行加权求和得到结果。具体来说，可以如下描述：

$$
\begin{align}
S &= Socre(Q,K)\\
W &= softmax(S)\\
Out &= \sum_i W_iV_i
\end{align}
$$

其中 $Score$ 是注意力评分函数。一般来说，有两种评分函数较为常用：点积注意力和加性注意力：

$$
\begin{align}
Score_{点积} (Q,K) &= \frac{QK^T}{\sqrt d}\\
Socre_{加性} (Q,K) &= \tanh(W_1Q+W_2K)V^T
\end{align}
$$

其中，$d$ 是向量维度，是为了防止矩阵过大而引入；$W_1$ 和 $W_2$ 则是可学习的参数。

多头注意力

在一族序列中，注意力可能有多个维度。而多头注意力通过将原有的查询和键值对通过全连接层进行变换，输入到多个注意力层中，并将各个注意力层的输出进行线性组合，从而增大了注意力机制提取信息的能力：

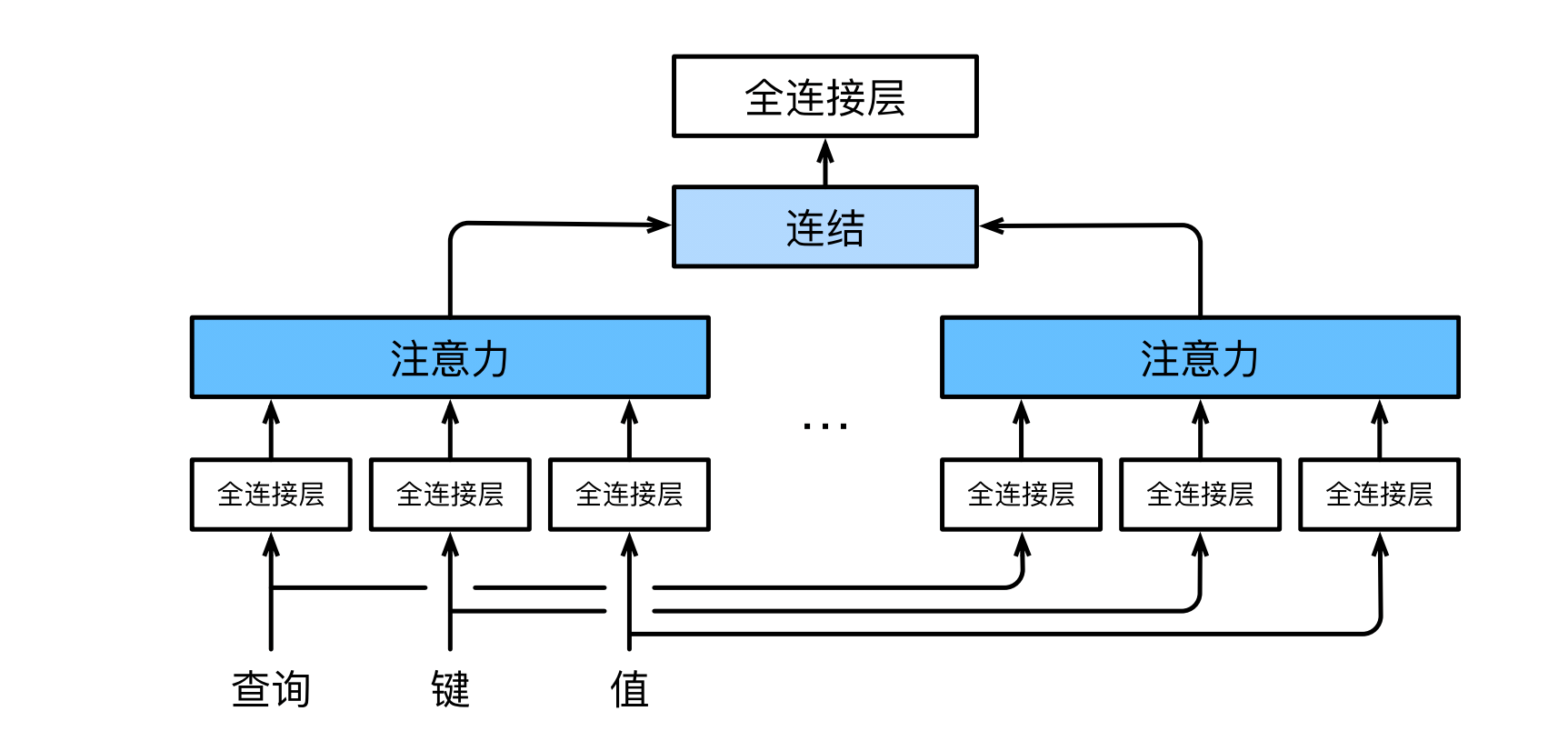
自注意力与位置编码

在序列处理中，我们可以将序列中的每一项 $X_i$ 同时视为键和值，即 $(K,V) = (X,X)$，这种网络称为自注意力。

但单纯应用自注意力没有意义，因为单独的 $X$ 并没有包含序列的顺序关系。换句话说，序列由哪些向量组成不重要，重要是向量的顺序是什么。因此，我们需要将位置编码进值$V$中。

对于输入 $X \in R^{n*d}$，位置编码输出 $X+P$，其中 $P$ 是位置嵌入矩阵，定义为：

$$
\begin{align}
P_{i,2j} = \sin(\frac i {10000^{2j/d}})\\
P_{i,2j+1} = \cos(\frac i {10000^{2j/d}})
\end{align}
$$

位置编码来源于数字的二进制表示。在二进制中，在数字增大的过程中，随着位数$i$增大，第$i$位会以更低的频率在0和1之间摆动：

而在位置编码中，$i$ 代表了位置，$j$ 代表了位数，因此将绝对位置编码了进去。

此外，位置编码还可以通过线性组合表达出相对位置。

残差连接和层归一化

在深度学习中，为了缓解梯度爆炸和梯度消失，可以使用残差连接。

残差连接将输入和原始输出相加作为新的输出，这样实际上有：

$$
O = f(x) + x
$$

而层归一化将输出向量在各个维度之间进行归一化，可以避免每一层的输出发生协变量偏移而导致性能下降：

$$
X_i = \frac{X_i-\mu}{\sqrt{\sigma^2+\epsilon}}
$$

其中 $\mu$ 和 $\sigma^2$ 是 $X$ 各维度的均值和方差。

Transformer 是完全基于注意力机制的Seq2Seq网络，使用Encoder-Decoder结构并包含多个相似的编解码器：

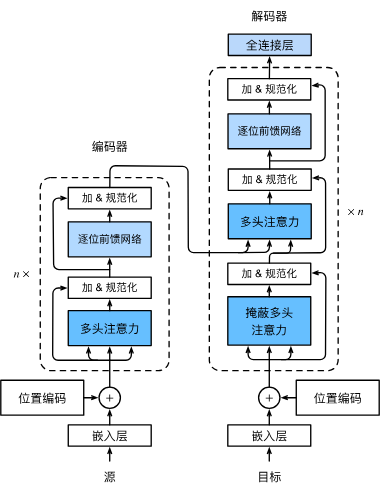
在transformer中，输入首先经过嵌入层转化并注入位置编码，然后进入$n$个编码器处理。每个编码器由一个多头自注意力层和一个逐位前馈网络组成，并在其之间使用残差连接和层规范化。多头自注意力提取出了序列中有用的信息，而前馈网络则将信息进行了整合。