关于Tarjan算法的理解
本文前置知识:图论基础
一.无向图中的Tarjan
在无向图中,Tarjan可以用来求割点与割边。
1.割点与割边
割点是指这样一类点:无向连通图 中,如果将其中一个点以及所有连接该点的边去掉,图就不再连通,这样的点称为割点。简单来说,就是删去后会让原来联通的图“分裂”成几个子图的点。孤立点不属于割点。
割边与之类似,即删去后,会把原图“分裂”成两个子图的点。割边又称“桥”。
e.g.
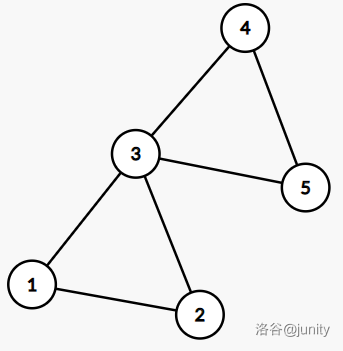
在这个图中,点4、2是割点,边3、4是割边。例如,点4删去后,原图会变成由点{2,3}和{1,5}构成的两个子图,而边4删去后,原图会变成{2,3}和{1,4,5}构成的两个子图。
相反的,点3和点5就不是割点。因为若删去,原图仍然是联通的。
2.搜索树、DFS序和时间戳
对于一个图来说,我们可以对其进行深度优先遍历,并按照遍历的顺序给每个点DFS序 。
而在深度优先遍历时形成的树形结构就称为这个图的一个搜索树。一个图可能有不止一个搜索树。
更为具体的,对图进行深度优先遍历,在遍历一个点的所有相邻点时,只选择那些没有被遍历过的点进行下一步遍历,最后遍历过的所有边就构成了这个图的一颗搜索树。搜索树上的边是有向的。
下面的代码求出一个无向图每个点的时间戳和DFS序:
int dfn[N],cnt = 0; //时间戳
int dfs_idx[N],tot = 0; //DFS序
void dfs(int x){
dfn[x] = ++cnt;
dfs_idx[++tot] = x;
for (int i = h[x]; i != -1; i = ne[i]) {
int y = e[i];
if (!dfn[y])
dfs(y);
}
}
对于一颗搜索树而言,它的一颗子树对应到DFS序上一定是连续的一段。
3.树边,非树边
对于一个图的一颗搜索树来说,它在搜索树上的边被称为树边,其余边称为非树边。
对于无向图,非树边只存在一种情况,即连接一个祖先节点和一个后代节点,不会出现连接两个不同子树的情况。因为如果连接了两个子树,那在遍历前一颗子树时,由于这条边的存在,会将另一颗子树也一起遍历掉,变成这颗子树的一个新子树(孙树?)。这条性质只在无向图中成立
e.g.(树边用黑色标注,非树边用红色)
原无向图:
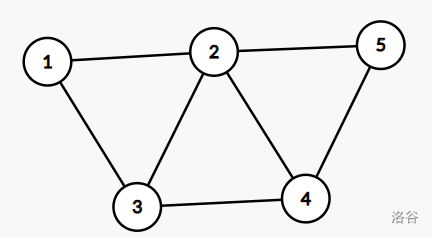
连接两颗子树的非树边
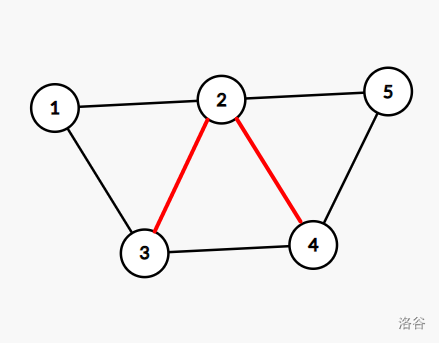
实际的遍历情况:
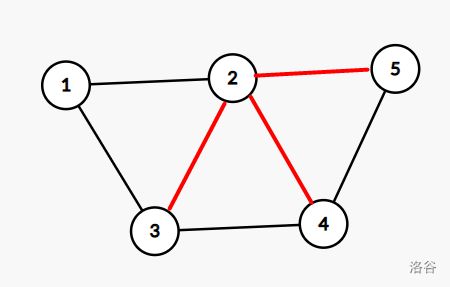
4.用Tarjan来求割点和割边
Tarjan算法的思想是,对于每个点
对于割边而言,方法也是类似:对于条搜索树上的边
具体来说,给每个点
综上,我们可以梳理出一个求割点和割边的流程:
- 通过DFS求出原图的一颗生成树,并标出时间戳
。 - 对于生成树上的每个节点,求出其追溯值
。 - 扫描所有点/边,根据上面的判定法则判定其是否是割点/割边。
在实现时,并不需要真的做3次DFS,因为在1次DFS中我们就可以完成所有流程。在求出所有子节点的追溯值后,该节点的追溯就可以通过求子节点追溯值的最小值求出。
模板:(以求割边为例)
int dfn[N],low[N],cnt; //cnt记录时间戳
vector<int> cut_edges;
void tarjan(int x,int in_edge){
dfn[x]=low[x]=++cnt;
for(int i=h[x];i!=-1;i=ne[i]){ //链式前向星存图
int y=e[i]; //y就是一个子节点
if(!dfn[y]){
tarjan(y); //dfn[y]为0表示y没有被遍历过
low[x]=min(low[x],low[y]);
if(dfn[x]<low[y]) //割边判定
cut_edges.push_back(i);
}
else if(i!=(in_edge^1)) //判断是否是从父节点下来的那条边,如果不是就代表是非树边。图中可能存在重边,
low[x]=min(low[x],dfn[y]); //不能直接判断y是否是父亲,故这里通过加边时无向图会加两次,编号只有二进制
//中最后一位不同来判断。
}
}
5.双联通分量 (DCC)
在无向图中,若一个图中不存在割点,则称为点双联通图;若不存在割边,则称为边双联通图。特别的,仅有一个点的图既属于点双联通图,又属于边双联通图;
一个图中的极大点双联通子图称为这个图的一个点双联通分量(v-DCC);类似的,一个图的极大边双联通子图称为这个图的一个边双联通分量(e-DCC)。e-DCC与v-DCC统称DCC。
需要注意的是,这里的“极大”指的并不是“最大”,而是说“不能更大”,即添加任何原图中的点/边后,都不能使得添加后的子图仍然是一个点/边双联通图。一个图可以有多个双联通分量。
在一个图中,任何一个点都属于且仅属于一个e-DCC,原因很简单:
- 一个点自身组成一个
e-DCC,说明每个点属于至少一个e-DCC - 若一个点同时属于多个
e-DCC,那么由于没有割边,故这些e-DCC可以合并为一个更大的边双联通图,与e-DCC定义中的"极大"相矛盾。
同样的,任何一个点都至少属于一个v-DCC,这与e-DCC的情况不同,如下图中:
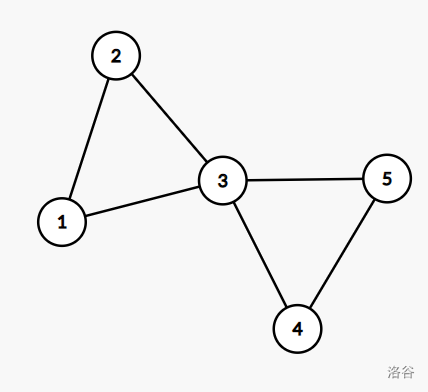
点v-DCC,而点v-DCC,点v-DCC。
6.e-DCC的求法和缩点
把e-DCC看成一个个的点,把割边看成这些点间连接的边,这样会形成一张新图。这种方法叫做缩点。
缩点后的图一定是一颗树或森林(如果原图不联通)。可以用反证法:若不是,则图中一定存在环;但存在环的话,这个环上的边就一定不是割边了,而我们的新图中的边全是由割边组成,故显然不成立。
求e-DCC,最简单的方法就是把割边全部删掉,然后找出所有的联通块了。在实现中,可以通过判断边是否是割边来实现,不需要真的删边。
缩点时,可以针对每一条原边,若边两端的点属于不同的DCC,则在这两个DCC中连一条边。
下面的代码在Tarjan求出割边后求出v-DCC并缩点。
int id[N]; //保存每个点属于的 v-DCC 编号
int dcc_cnt; //保存 v-DCC 个数
void dfs(int x,int id){
id[x]=id;
for(int i=h[x];i!=-1;i=ne[i]){
int y=e[i];
if(!id[y] || is_bridge[i])
dfs(y,id);
}
}
//主函数中
//找出 v-DCC
for(int i=1;i<=n;i++) //遍历所有点
if(!id[i]) //判断是否遍历过
dfs(i,++dcc_cnt);
//缩点
for(int x=1;x<=n;x++) //遍历所有点
for(int i=h[x];i!=-1;i=ne[i]){ //遍历该点所有边
int y=e[i];
if(id[x]!=id[y])
add_c(id[x],id[y]); //add_c 意为在新图中连边
}
7.v-DCC的求法和缩点
求法
v-DCC的求法比e-DCC要复杂,原因就是一个点会属于不同的v-DCC,我们不能直接把所有的割点删除后计算联通块。
可以发现,只有割点会属于多个v-DCC,证明如下:
设该点为 v-DCC,且 v-DCC仍然联通,故可组成一个更大的v-DCC,与v-DCC的“极大”矛盾,故不成立。
那么我们可以在找到割点时,同时找出其属于的所有v-DCC。
具体来说,我们可以维护一个栈,当 Tarjan 进入到一个点 v-DCC,此时将它们出栈并记录即可(x 不出栈)。代码如下:
int stack[N], top, dfn[N], low[N], cnt, id[N];
int cnt[N];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
stack[++top] = x;
if (x == root && head[x] == 0) { // 孤立点
dcc[++cnt].push_back(x);
return;
}
int flag = 0; // flag记录子树个数
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
flag++;
if (x != root || flag > 1)
cut[x] = true;
cnt++;
int z;
do {
z = stack[top--];
dcc[cnt].push_back(z);
} while (z != y);
dcc[cnt].push_back(x);
}
}
else
low[x] = min(low[x], dfn[y]);
}
}
PS:其实这段代码来自蓝书 Github链接
下面来证明一下这个做法的正确性:
首先,由于节点按照DFS的顺序入栈,故栈中在上方的点的时间戳要比下方的时间戳大。因此,对于一个割点
然后来证明,当一个割点 v-DCC,且组成整个完整的v-DCC的。先证明他们属于同一个v-DCC:
- 若不属于同一个
v-DCC,则其中肯定存在割点,和割点连接的另一个v-DCC中的点。 - 然而,由于我们在找到割点时就将它的子树里属于其他
v-DCC的节点全部出栈了,因为显然割点属于的v-DCC要么在子树中,要么是祖先节点那边的,故不可能有其他v-DCC中的点了。
接着证明里面包含了这个v-DCC全部的点:
- 根据定义,如果找不到其他点可以加到这个
v-DCC中,并保持它双联通的性质不变,那么这些点就构成了完整的v-DCC。 - 而在栈中的点,分成三种情况:
- 叶子节点,这些点不能再延伸出其他点了。
- 割点,它的子节点要么因为判定法则成立、被出栈,这些点添加进来会破坏
v-DCC的性质;要么就是在栈中的点。 - 其他点,这些点连的每条边都延伸出去了,没有点可以再延伸了。
- 因此,栈中的点一定无法再延伸出其他点了。
综上,当判定法则成立时,栈中在 v-DCC。
缩点
v-DCC的缩点也要复杂一点。假设求出了v-DCC,有v-DCC,因此缩点后,新图中的节点数为
e.g.
这是缩点前的图,其中3号点是一个割点:

缩点后:
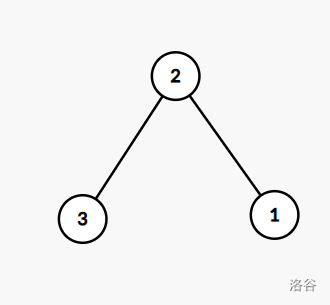
其中,3号点代表原图中v-DCC,1号点代表原图中v-DCC,而2号点代表原图中的割点3号点。
可以发现,缩点后的每个v-DCC实际上都是通过割点相连接的,每两个v-DCC缩点后至少隔了一个割点。
于是可以得到以下缩点步骤:
-
对于每个
v-DCC,建立一个点,并对每个割点也建立一个点。 -
遍历每个
v-DCC,对于其中的每个割点,连一条该v-DCC到割点的边。
代码如下:
int id[N],cnt;
int cut[N];
vector<int> dcc;
int n; //n为点数
void add_c(int a,int b); // 自己定义的在新图里面加边的函数
... //使用tarjan求出了v-DCC,并标出了每个点对应的v-dcc编号存在id[x]里面。
//cut里面存每个点是不是割点。
//dcc里面存每个dcc里面的点。
/* 以上变量应已经求出 */
int new_id[N],num; //new_id 保存每个割点对应新点的编号
num = cnt; //方便起见,编号从cnt开始,就不用再给每个v-dcc也赋新编号了
for(int i=1;i<=n;i++) //给每个割点取新编号
if(cut[i])
new_id[i] = num++;
for(int i=1;i<=cnt;i++){ //遍历每个v-DCC
for(int j:dcc[i]){ //遍历这个v-DCC里面的所有点,使用C++11的语法糖。
if(cut[j]){
add_c(new_id[j],i);
add_c(i,new_id[j]);
}
}
}
二.有向图中的 Tarjan
1.强连通分量 (SCC)
有向图中,若一个图中任意两个点
简单来说,强联通图就是任意两个点可以互相到达的图,强连通分量就是有向图的一个极大强联通子图。
e.g.
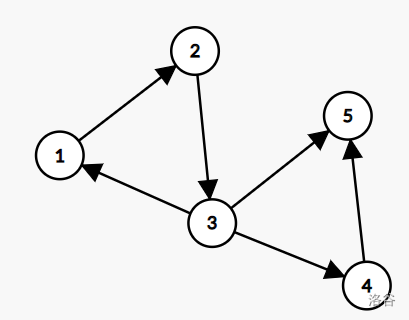
这张图中,点
一个点只能属于一个SCC,因为如果同时属于两个SCC,设其为 SCC中分别任取一个点,都可以先到 SCC可以合并为一个。
2.搜索树、DFS序和时间戳 in 有向图
与无向图类似,有向图也有搜索树、时间戳的概念,这里不在赘述。同样的,记点
3.前向边,后向边,树枝边,横叉边
对于一个有向图,我们将其上的有向边
- 树枝边:在搜索树上的边,即
是 的父节点。 - 前向边:
是 的后代节点。 - 后向边:
是 的祖先节点。 - 横叉边:
、 不存在祖先后代关系(比如你和你堂弟?)。此时一定有 ,理由和无向图非树边那的证明差不多。
4.SCC的判定
考虑什么情况下几个点会组成SCC。显然,成环时,环上的点一定是强联通的:只要走不超过一圈,必然可以到达其他所有的点。
而如果一个SCC由多个点组成,那么其中的任意一点
因此,我们只需要找环就可以了。
再考虑什么时候会存在环:显然,在所有边中,后向边一定代表了一个环。而横叉边有可能能成环,这取决于另外一个点。
综上,我们建立一个栈,在DFS遍历到
容易发现,因为有后向边的存在,
的祖先节点 - 通过后向边可以到
的祖先的点。
同时引入追溯值的概念:节点
我们这样维护栈:
- 当一个节点被DFS遍历到时,把它入栈
- 当一个节点满足
时,它和栈中它上方的点组成一个强连通分量,此时把它与它上面的点出栈并记录。
同时这也是强联通分量的判定法则:当节点满足
先看下代码吧:
int dfn[N],low[N],num; //注意这里的low与上文说的low有一定出入,下文会说
int stack[N],top,ins; //ins代表节点是否在栈中
int c[N]; //c[x]表示x对应的SCC的编号
vector<int> scc; //保存每个scc中的点
int cnt; //保存scc编号分到第几个了
void tarjan(int x) {
dfn[x] = low[x] = ++num;
stack[++top] = x, ins[x] = 1;
for (int i = head[x]; i; i = Next[i])
if (!dfn[ver[i]]) {
tarjan(ver[i]);
low[x] = min(low[x], low[ver[i]]);
}
else if (ins[ver[i]])
low[x] = min(low[x], dfn[ver[i]]);
if (dfn[x] == low[x]) {
cnt++; int y;
do {
y = stack[top--], ins[y] = 0;
c[y] = cnt, scc[cnt].push_back(y);
} while (x != y);
}
}
PS:同样来自蓝书,改了一点点。
现在来说明为什么是正确的。
先不考虑维护
证明:
如果栈中有点不能走到
的后代中没有可以走到比 更上面的点了,此时 ,这些点被弹出了。 的后代中有可以走到更上面的点,那么 可以先到 ,再到更上面的点,故 ,与原设矛盾。
因此,这些点都可以走到 SCC。
再证明这个SCC里面的点都在栈中。
如果有其他点属于这个SCC,设这个点为 SCC,
综上,如果 SCC。
再考虑代码中的维护过程:
实际上,Tarjan算法忽略了一个无关的问题,即在:
的后代中有可以走到更上面的点,那么 可以先到 ,再到更上面的点,故 ,与原设矛盾。
这种情况下没有更新
为什么说无关呢?
回到上面的推导,我们要保证的是栈中的元素都可以到
对于
因此,只要 y 可以到 x,那么在 x 之前 y 就不会被弹出
如果有其他点属于这个
SCC,设这个点为,那么因为属于一个 SCC,一定可以到 ,即 ,故 在 之前不会被弹出,一定在栈中。
而
综上,代码中的维护方式不会对结果产生影响。
5.SCC的缩点
SCC 的缩点与DCC类似,但不同的是 SCC 缩点后会形成 有向无环图。
缩点的方式与e-DCC的缩点类似,只需要将原图中连接两个不同 SCC 的边加进去就可以了。
代码:
int id[N]; //原图中每个点对应SCC的编号
void add_c(int a,int b); //自己定义的在新图中加边的函数
for(int x=1;x<=n;x++){ //遍历所有点
for(int i=h[x];i!=-1;i=ne[i]){
int y=e[i];
if(id[x]!=id[y])
add_c(id[x],id[y]);
}
}
** 全文完 **




Comments NOTHING